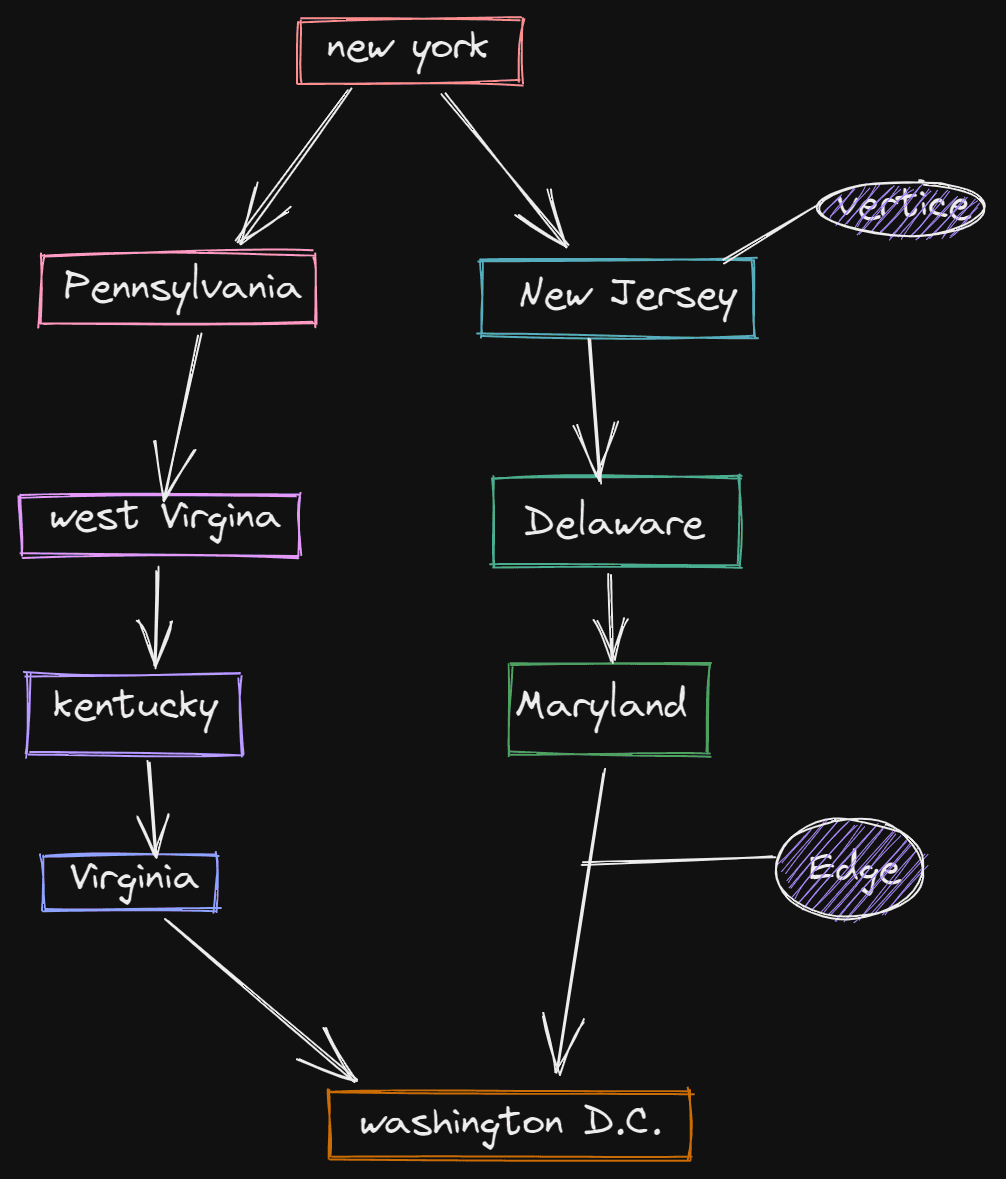
A Graph is a non linear data structure that consists of edges and vertices. A vertice is the data stored in memory and the edge is the pointer that describes the connection between two vertices.

Overview

States that will be cross during a road trip from New York to Washington D.C.

Time Complexity

Space Complexity

The Vertex

The Vertex is the building block of a Graph, and it is the element that contains the data.

public class Vertex<T> {
    private final T value;
}

Graph implementation

One way to implement a Graph is to have a Map of Vertices and Edges. The Edges can be represented as a List that is related to a vertice.

public class Graph<T> {
    private Map<Vertex<T>, List<Vertex<T>>> adjVertices;

    public Graph() {
        adjVertices = new HashMap<>();
    }
}

Below is the Graph representation of the road trip example.

Add Vertex

To Add a vertex, we can simply add it to the map.

public class Graph<T> {
    private Map<Vertex<T>, List<Vertex<T>>> adjVertices;

    public Graph() {
        adjVertices = new HashMap<>();
    }

    public void addVertex(final T value) {
        adjVertices.putIfAbsent(new Vertex<>(value), new ArrayList<>());
    }
}

At this point, we can add all the potential states we will cross over as vertexes.

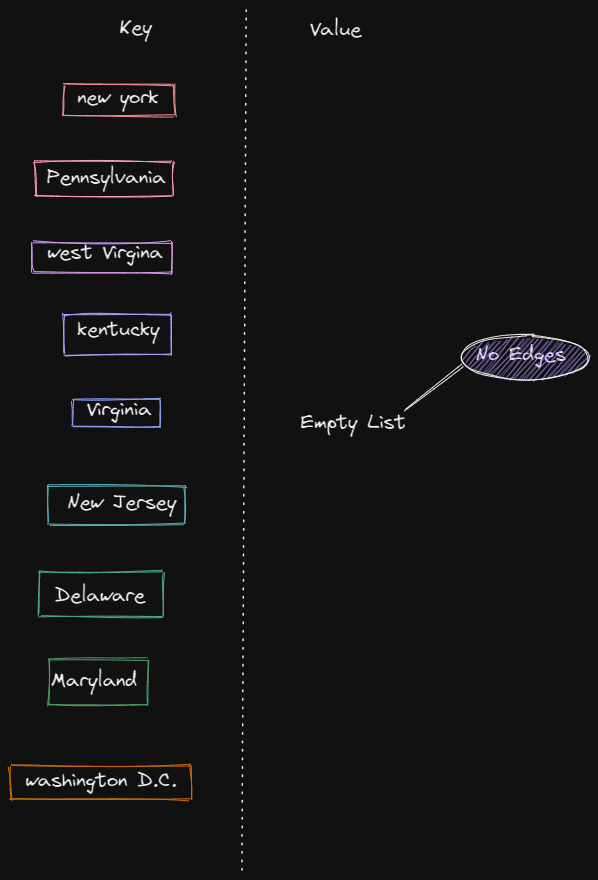
Add Edge

A graph with vertices only is not very useful, edges is what powers a graph. The following code can add edges to a vertices.

public class Graph<T> {
    private Map<Vertex<T>, List<Vertex<T>>> adjVertices;

    public Graph() {
        adjVertices = new HashMap<>();
    }

    public void addEdge(final T value1, final T value2) {
        final Vertex<T> vertex1 = new Vertex<>(value1);
        adjVertices.get(vertex1).add(vertex2);
    }
}

Graph Traversal - Depth First Search

When applying depth first search, we are going to traverse each branch all the way to the end before beginning to explore the next branch.

The algorithm for DFS is simple, we are going to traverse each node and for each node’s children we are going to call the DFS function

When to use Depth First Search

1. When the tree is very wide.
2. If solutions are located deep in the tree.

    List<String> dfs(final Graph<String> graph, final String root, final List<String> visited) {
        visited.add(root);
        final List<Vertex<String>> vertices = graph.getAdjVertices(root);

        for(Vertex<String> vertex : vertices) {
            if(!visited.contains(vertex.getValue())) {
                dfs(graph,vertex.getValue(),visited);
            }
        }


        return visited;
    }

Graph Traversal - Breath First Search

When applying breath first search, we are going to traverse the graph, level by level. We start at the top level and then traverse to the next level.

The difference of BFS and DFS, is that in DFS we traverse from top to bottom branch by branch. In BFD, we traverse from left to right, level by level.

List<String> visited = new ArrayList<>();

      final Queue<String> queue = new LinkedList<>();

        queue.add("A");

        while(!queue.isEmpty()) {
            final String itemPopped = queue.remove();

            final List<Vertex<String>> vertices = graph.getAdjVertices(itemPopped);

            if(!visited.contains(itemPopped)) {
                visited.add(itemPopped);
            }

            vertices.forEach(vertex -> {
                if(!visited.contains(vertex.getValue())) {
                    queue.add(vertex.getValue());
                }
            });
        }

When to use Breath First Search

1. If you know the solutions is close to the root.
2. If the tree is very deep.

Conclusion

Every dance is a kind of fever chart a graph of the heart.

Martha Graham