Write an algorithm that takes in an array of integers and returns a sorted version of that array, using MergeSort.

Overview

Merge Sort is a divide & conquer algorithm. What that means is that, MergeSort divides an array and then conquers the two halves arrays. Conquering meaning that the array will be sorted. MergeSort continuously divides the array and then sorts those sub arrays.

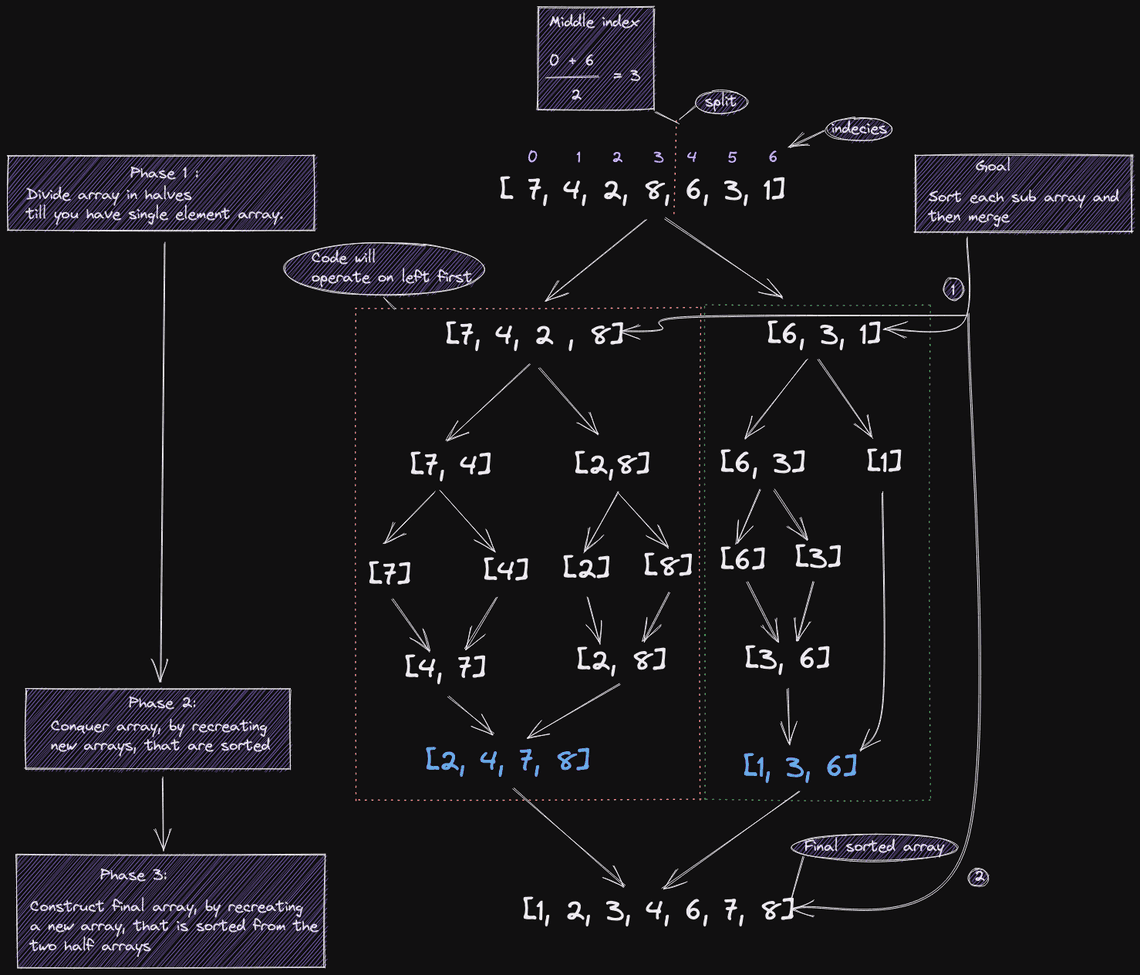
Solution

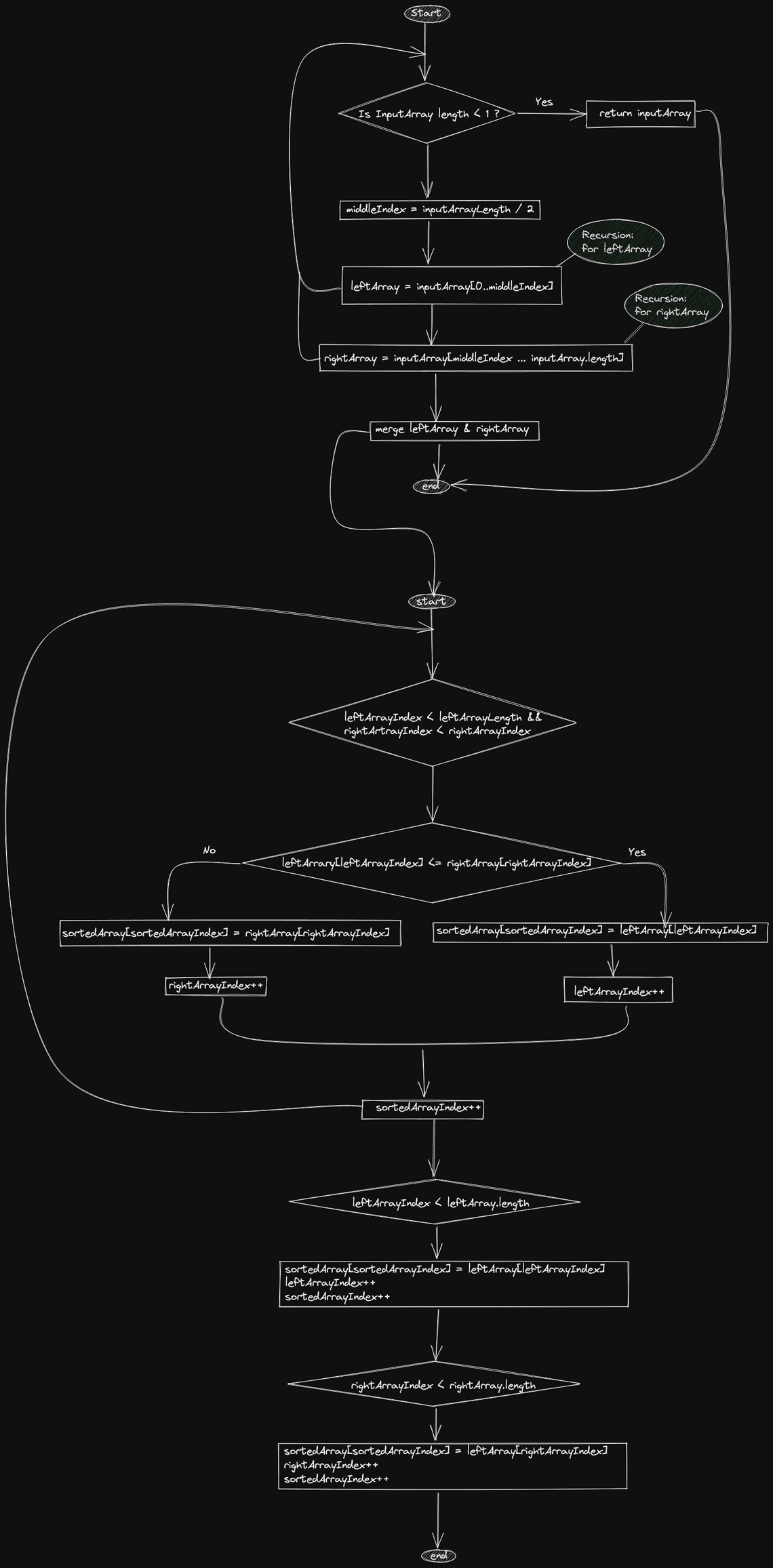
The diagram on its own provides half the value of understanding the MergeSort algorithm, to compliment the solution, the Java Source code on this page will provide a complete picture of the MergeSort algorithm.

Time Complexity

To analyze the time complexity of Merge Sort, we need to look in detail how it operates. The MergeSort overview diagram shows how the array was divided four times. At each level of dividing, takes O(N), constant time. All we would have to do now is add up the time complexity of each level and that should give us the total time complexity. Because we divide the array in half and then further divide in half, we get logN levels in MergeSort, ultimately giving us a total time complexity of O(nlogn)

Space Complexity

Similarly as with time complexity, at each level of merge sort, as the array is divided, we create a new array of size N, therefore O(n). This leads to a grand total Space Complexity of O(nlogn). This is not great, because we are creating new arrays with similar data at each level. What if we can sort the array in place and not create a new array. That can give us a nice time complexity O(n). There is a way to solve that and that solution will be in part 2 of the MerseSort algorithm overview.

Java Source Code

    public int[] sort(final int[] inputArray) {
        if (inputArray.length == 1) {
            return inputArray;
        }

        final int middleIndex = inputArray.length / 2;
        final int[] leftArray = Arrays.copyOfRange(inputArray, 0, middleIndex);
        final int[] rightArray = Arrays.copyOfRange(inputArray,middleIndex,inputArray.length);
        final int[] sortedLeftArray = sort(leftArray);
        final int[] sortedRightArray = sort(rightArray);

        return merge(sortedLeftArray,sortedRightArray);
    }

    private int[] merge(final int[] leftArray, final int[] rightArray) {
        final int[] sortedArray = new int[leftArray.length+rightArray.length];
        int leftArrayIndex = 0;
        int rightArrayIndex = 0;
        int sortedArrayIndex=0;

        while (leftArrayIndex < leftArray.length && rightArrayIndex < rightArray.length) {

            if(leftArray[leftArrayIndex] <= rightArray[rightArrayIndex]) {
                sortedArray[sortedArrayIndex] = leftArray[leftArrayIndex];
                leftArrayIndex++;
            } else {
                sortedArray[sortedArrayIndex] = rightArray[rightArrayIndex];
                rightArrayIndex++;
            }

            sortedArrayIndex++;
        }

        while(leftArrayIndex < leftArray.length) {
            sortedArray[sortedArrayIndex] = leftArray[leftArrayIndex];
            leftArrayIndex++;
            sortedArrayIndex++;
        }

        while(rightArrayIndex < rightArray.length) {
            sortedArray[sortedArrayIndex] = rightArray[rightArrayIndex];
            rightArrayIndex++;
            sortedArrayIndex++;
        }

        return sortedArray;
    }

Conclusion

I don’t like looking back. I’m always constantly looking forward. I’m not the one to sort of sit and cry over spilt milk. I’m too busy looking for the next cow.

Gordon Ramsay