Given an integer array arr, return the length of the longest subarray, which is a peak.

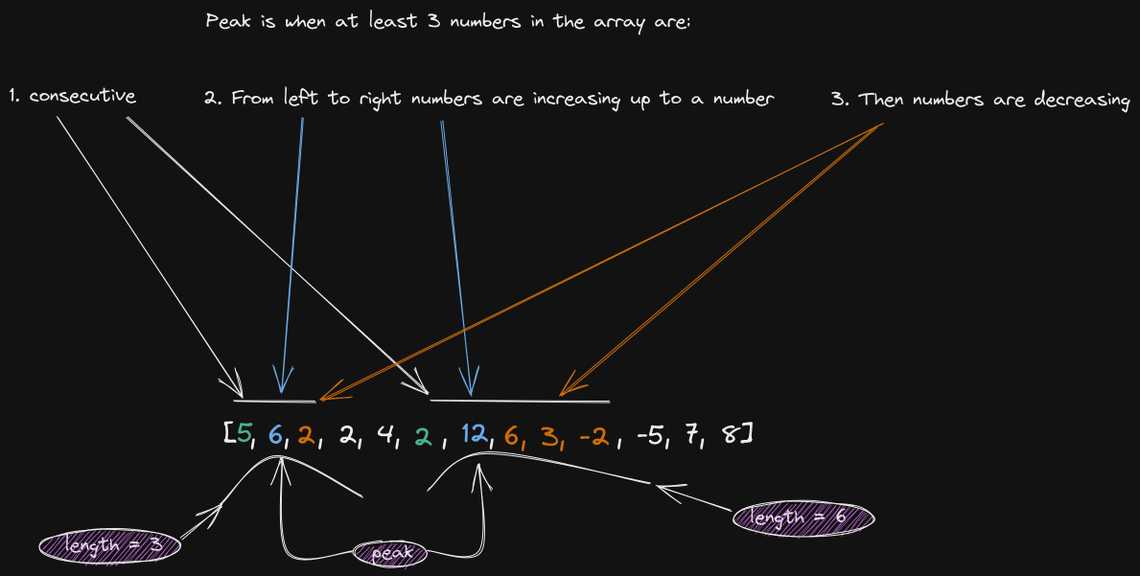
A peak is:

- array.length >= 3
- There exists some index i (0-indexed) with 0 < i < arr.length - 1 such that:
    - array[0] < array[1] < ... < array[i - 1] < array[i]
    - array[i] > array[i + 1] > ... > array[array.length - 1]

Overview

Optimal Solution

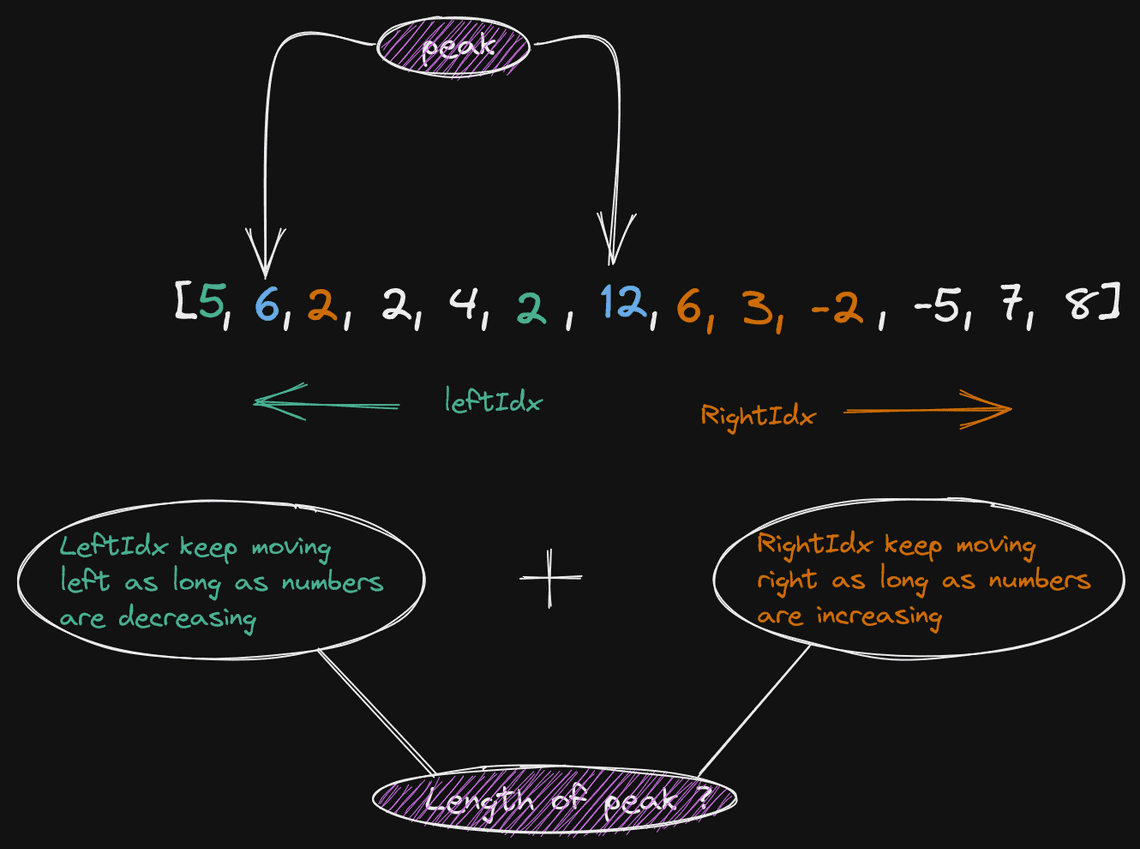
The essence here is that, once we find a peak, then keep expanding on both directions of the element until there is no longer a peak.

Flow Diagram

Time Complexity

As we are traversing the whole array once, the time complexity is O(n). No other complex operation needed.

Space Complexity

Space complexity will be a constant time of O(1), no extra space needed.

Java Source Code

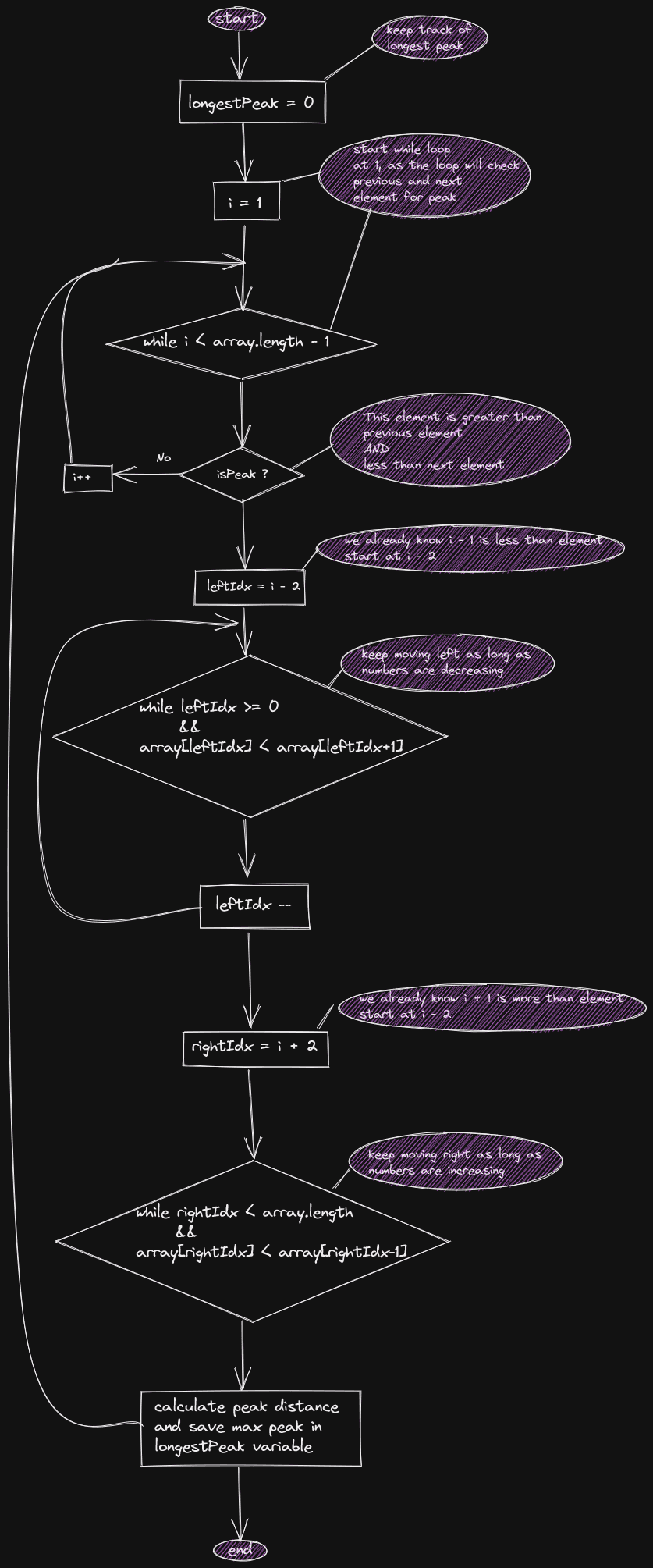
   public int find(int[] array) {
        var longestPeakLength = 0;

        var i = 1;
        while (i<array.length-1) {
            var isPeak = array[i-1] < array[i] && array[i] > array[i+1];

            if(!isPeak) {
                i++;
                continue;
            }

            var leftIdx = i -2;

            while(leftIdx >= 0 && array[leftIdx] < array[leftIdx+1]) {
                leftIdx--;
            }

            var rightIdx = i + 2;

            while (rightIdx < array.length && array[rightIdx] < array[rightIdx-1]) {
                rightIdx++;
            }

            var currentPeakLength = rightIdx - leftIdx - 1;
            longestPeakLength = Math.max(longestPeakLength,currentPeakLength);

            i=rightIdx;
        }

        return longestPeakLength;
    }

Conclusion

You need to think outside the box. You need to think differently if you want to sustain what, for me, is my peak performance: the very best that I can achieve as an athlete every day.

Tom Brady